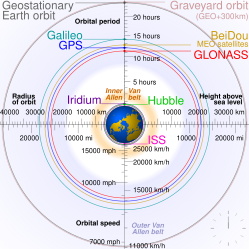
Geostationary orbit
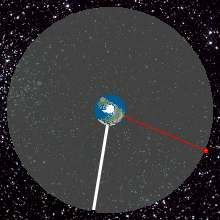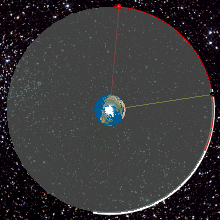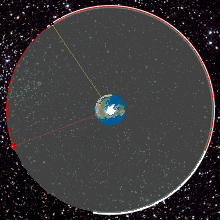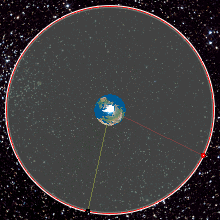
Geostationary orbits (top view). To an observer on the rotating Earth,
both satellites appear stationary in the sky at their respective
locations.

Geostationary orbits (side view)

A 5 × 6 degree view of a part of the geostationary belt, showing several
geostationary satellites. Those with inclination 0 degrees form a
diagonal belt across the image; a few objects with small inclinations to
the
Equator are visible above this line. The satellites are pinpoint, while stars have created small trails due to the
Earth's rotation.
A
geostationary orbit,
geostationary Earth orbit or
geosynchronous equatorial orbit[1] (
GEO),
is an orbit whose position in sky remains the same for a stationary
observer on earth. This effect is achieved with a circular
orbit 35,786 kilometres (22,236 mi) above the Earth's
equator and following the direction of the Earth's rotation.
[2] An object in such an orbit has an
orbital period equal to the Earth's rotational period (one
sidereal day), and thus appears motionless, at a fixed position in the sky, to ground observers.
Communications satellites and
weather satellites are often placed in geostationary orbits, so that the
satellite antennas
which communicate with them do not have to move to track them, but can
be pointed permanently at the position in the sky where they stay. Using
this characteristic, ocean color satellites with visible sensors (e.g.
the
Geostationary Ocean Color Imager (GOCI)) can also be operated in geostationary orbit in order to monitor sensitive changes of ocean environments.
A geostationary orbit is a particular type of
geosynchronous orbit,
the distinction being that while an object in geosynchronous orbit
returns to the same point in the sky at the same time each day, an
object in geostationary orbit never leaves that position.
The notion of a
geosynchronous satellite for communication purposes was first published in 1928 (but not widely so) by
Herman Potočnik.
[3] The first appearance of a geostationary
orbit in popular literature was in the first
Venus Equilateral story by
George O. Smith,
[4] but Smith did not go into details. British
science fiction author Arthur C. Clarke
disseminated the idea widely, with more details on how it would work,
in a 1945 paper entitled "Extra-Terrestrial Relays — Can Rocket Stations
Give Worldwide Radio Coverage?", published in
Wireless World magazine. Clarke acknowledged the connection in his introduction to
The Complete Venus Equilateral.
[5] The orbit, which Clarke first described as useful for broadcast and relay communications satellites,
[6] is sometimes called the
Clarke Orbit.
[7] Similarly, the
Clarke Belt is the part of space about 35,786 km (22,236 mi) above
sea level,
in the plane of the Equator, where near-geostationary orbits may be
implemented. The Clarke Orbit is about 265,000 km (165,000 mi) long.
Practical uses
Most commercial
communications satellites,
broadcast satellites and
SBAS satellites operate in geostationary orbits. A
geostationary transfer orbit is used to move a satellite from
low Earth orbit (LEO) into a geostationary orbit. (
Russian television satellites have used
elliptical Molniya and
Tundra orbits due to the high latitudes of the receiving audience.) The first satellite placed into a geostationary orbit was the
Syncom-3, launched by a
Delta-D rocket in 1964.
A worldwide network of operational geostationary meteorological
satellites is used to provide visible and infrared images of Earth's
surface and atmosphere. These satellite systems include:
A
statite, a hypothetical satellite that uses a
solar sail
to modify its orbit, could theoretically hold itself in a geostationary
"orbit" with different altitude and/or inclination from the
"traditional" equatorial geostationary orbit.
Orbital stability
A geostationary orbit can only be achieved at an altitude very close
to 35,786 km (22,236 mi), and directly above the Equator. This equates
to an orbital velocity of 3.07 km/s (1.91 mi/s) or a period of 1,436
minutes, which equates to almost exactly one
sidereal day or 23.934461223 hours. This ensures that the satellite is locked to the Earth's rotational period and has a stationary
footprint on the ground. All geostationary satellites have to be located on this ring.
A combination of
lunar gravity,
solar
gravity, and the flattening of the Earth at its poles causes a
precession motion of the orbital plane of any geostationary object, with
a period of about 53 years and an initial inclination gradient of about
0.85 degrees per year, achieving a maximum inclination of 15 degrees
after 26.5 years. To correct for this
orbital perturbation, regular
orbital stationkeeping manoeuvres are necessary, amounting to a
delta-v of approximately 50 m/s per year.
A second effect to be taken into account is the longitude drift,
caused by the asymmetry of the Earth – the Equator is slightly
elliptical. There are two stable (at 75.3°E, and at 104.7°W) and two
unstable (at 165.3°E, and at 14.7°W) equilibrium points. Any
geostationary object placed between the equilibrium points would
(without any action) be slowly accelerated towards the stable
equilibrium position, causing a periodic longitude variation. The
correction of this effect requires
orbit control manoeuvres with a maximum delta-v of about 2 m/s per year, depending on the desired longitude.
Solar wind and radiation pressure also exert small forces on
satellites which, over time, cause them to slowly drift away from their
prescribed orbits.
In the absence of servicing missions from the Earth or a renewable
propulsion method, the consumption of thruster propellant for
station-keeping places a limitation on the lifetime of the satellite.
Communications
Satellites in geostationary orbits are far enough away from Earth
that communication latency becomes significant — about a quarter of a
second for a trip from one ground-based transmitter to the satellite and
back to another ground-based transmitter; close to half a second for a
round-trip communication from one Earth station to another and then back
to the first.
For example, for ground stations at
latitudes of
φ = ±45° on the same
meridian as the satellite, the time taken for a signal to pass from Earth to the satellite and back again can be computed using the
cosine rule, given the geostationary orbital radius
r (derived below), the
Earth's radius R and the
speed of light c, as

(Note that
r is the orbital radius, the distance from the centre of the Earth, not the height above the Equator.)
This delay presents problems for latency-sensitive applications such as voice communication.
[8]
Geostationary satellites are directly overhead at the Equator, and
become lower in the sky the further north or south one travels. As the
observer's latitude increases, communication becomes more difficult due
to factors such as atmospheric refraction, Earth's thermal emission,
line-of-sight obstructions, and signal reflections from the ground or
nearby structures. At latitudes above about 81°, geostationary
satellites are below the horizon and cannot be seen at all.
[9]
Orbit allocation
Satellites in geostationary orbit must all occupy a single ring above the
Equator.
The requirement to space these satellites apart to avoid harmful
radio-frequency interference during operations means that there are a
limited number of orbital "slots" available, thus only a limited number
of satellites can be operated in geostationary orbit. This has led to
conflict between different countries wishing access to the same orbital
slots (countries near the same
longitude but differing
latitudes) and radio frequencies. These disputes are addressed through the
International Telecommunication Union's allocation mechanism.
[10][11]
In the 1976 Bogotá Declaration, eight countries located on the Earth's
equator claimed sovereignty over the geostationary orbits above their
territory, but the claims gained no international recognition.
[12]
Limitations to usable life of geostationary satellites
When they run out of thruster fuel, the satellites are at the end of
their service life as they are no longer able to keep in their allocated
orbital position. The transponders and other onboard systems generally
outlive the thruster fuel and, by stopping N-S station keeping, some
satellites can continue to be used in
inclined orbits (where the orbital track appears to follow a figure-eight loop centred on the Equator),
[13][14] or else be elevated to a "graveyard"
disposal orbit.
Derivation of geostationary altitude
In any circular orbit, the
centripetal force required to maintain the orbit (F
c) is provided by the gravitational force on the satellite (F
g). To calculate the geostationary orbit altitude, one begins with this equivalence:
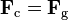
By
Newton's second law of motion,
[15] we can replace the forces
F with the
mass m of the object multiplied by the
acceleration felt by the object due to that force:
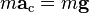
We note that the mass of the satellite
m appears on both sides — geostationary orbit is independent of the mass of the satellite.
[c] So calculating the altitude simplifies into calculating the point where the magnitudes of the
centripetal acceleration required for orbital motion and the
gravitational acceleration provided by Earth's gravity are equal.
The
centripetal acceleration's magnitude is:

where
ω is the
angular speed, and
r is the orbital radius as measured from the Earth's center of mass.
The magnitude of the
gravitational acceleration is:

where
M is the mass of Earth,
5.9736 × 1024 kg, and
G is the
gravitational constant,
6.67428 ± 0.00067 × 10−11 m3 kg−1 s−2.
Equating the two accelerations gives:
![r^3 = \frac{G M}{\omega^2} \to r = \sqrt[3]{\frac{G M}{\omega^2}}](http://upload.wikimedia.org/math/f/1/6/f16eada220130a499e9ee74aaa4d4fe4.png)
The product
GM is known with much greater precision than either factor alone; it is known as the
geocentric gravitational constant μ =
398,600.4418 ± 0.0008 km3 s−2:
![r = \sqrt[3]{\frac\mu{\omega^2}}](http://upload.wikimedia.org/math/2/e/d/2ed5811b0801300d18f371bcd649d54c.png)
The angular speed
ω is found by dividing the angle travelled
in one revolution (360° = 2π rad) by the orbital period (the time it
takes to make one full revolution). In the case of a geostationary
orbit, the orbital period is one
sidereal day, or
86,164.09054 seconds).
[16] This gives:
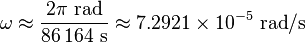
The resulting orbital radius is 42,164 kilometres (26,199 mi). Subtracting the
Earth's equatorial radius, 6,378 kilometres (3,963 mi), gives the altitude of
35,786 kilometres (22,236 mi).
Orbital speed (how fast the satellite is moving through space) is
calculated by multiplying the angular speed by the orbital radius:
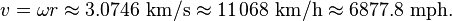
By the same formula we can find the geostationary-type orbit of an object in relation to
Mars (this type of orbit above is referred to as an
areostationary orbit if it is above Mars). The
geocentric gravitational constant GM (which is μ) for Mars has the value of 42,828 km
3s
−2, and the known
rotational period (
T) of Mars is 88,642.66 seconds. Since ω = 2π/
T, using the formula above, the value of ω is found to be approx 7.088218×10
−5 s
−1. Thus,
r3 = 8.5243×10
12 km
3, whose cube root is 20,427 km; subtracting the equatorial radius of Mars (3396.2 km) we have 17,031 km.





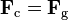
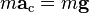


![r^3 = \frac{G M}{\omega^2} \to r = \sqrt[3]{\frac{G M}{\omega^2}}](http://upload.wikimedia.org/math/f/1/6/f16eada220130a499e9ee74aaa4d4fe4.png)
![r = \sqrt[3]{\frac\mu{\omega^2}}](http://upload.wikimedia.org/math/2/e/d/2ed5811b0801300d18f371bcd649d54c.png)
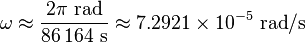
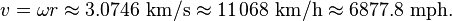


 is orbital velocity of orbiting body,
is orbital velocity of orbiting body, is radius of the circle
is radius of the circle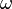 is angular speed, measured in radians per second.
is angular speed, measured in radians per second.
 is the standard gravitational parameter.
is the standard gravitational parameter.
 is specific angular momentum of the orbiting body.
is specific angular momentum of the orbiting body.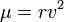 again.
again.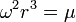
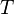 ) can be computed as:
) can be computed as: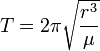
 (17.7 % of the orbital period in a circular orbit)
(17.7 % of the orbital period in a circular orbit) (7.5 % of the orbital period in a circular orbit)
(7.5 % of the orbital period in a circular orbit) ) is negative, and
) is negative, and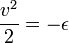

 is given by the following formula:
is given by the following formula: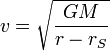
 is the Schwarzschild radius of the central body.
is the Schwarzschild radius of the central body. .
.
 is constant on a circular orbit, and the coordinates can be chosen so that
is constant on a circular orbit, and the coordinates can be chosen so that  ). The dot above a variable denotes derivation with respect to proper time
). The dot above a variable denotes derivation with respect to proper time  .
.
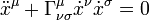
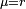 . It gives:
. It gives: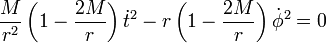

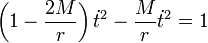

 , who is not moving with respect to the central body, that is, his four-velocity is proportional to the vector
, who is not moving with respect to the central body, that is, his four-velocity is proportional to the vector  . The normalization condition implies that it is equal to:
. The normalization condition implies that it is equal to: